Testing DB Normalization Theory vs Practice - FDSampleRush
Introduction
Database normalization is a fundamental process in database design, ensuring data integrity and minimizing redundancy. Despite its theoretical foundations, practical implications and occurrences of different normal forms in real-world databases are underexplored. Our recent work addresses this gap by developing FDSampleRush, a tool that uses Monte Carlo simulations to generate and analyze the distribution of normal forms given functional dependencies. We also provide a basic use case to challenge whether it is reasonable to enforce BCNF-level normalization on any schema.
This mini-research was a collaborative effort by me, Lee Jia Sheng, and Radhya Fawza for our CS4221 (Database Apps Design and Tuning) project. Together, we aimed to bridge the gap between theoretical database normalization and its practical applications.
What is Database Normalization?
Before diving into our findings, let’s briefly discuss what database normalization is and why it’s important. Imagine you have a table of employee data in a company:
| EmployeeID | Name | Department | DepartmentHead |
|---|---|---|---|
| 1 | Alice | HR | Bob |
| 2 | Charlie | IT | Dave |
| 3 | Eve | HR | Bob |
Without normalization, you might store the department head’s name in every row. This redundancy can lead to inconsistencies. If Bob leaves the company and someone forgets to update one of the rows, your data is now inaccurate. Normalization aims to reduce such redundancy.
What is FDSampleRush?
FDSampleRush is an open-source tool designed to generate and analyze the distribution of normal forms in relational schemas. By systematically creating random sets of functional dependencies (FDs), this tool allows researchers to study how theoretical normal forms manifest in practice. This can offer insights into whether the rigorous pursuit of higher normal forms, like BCNF, is always necessary.
Key Findings
Through extensive simulations, we found that achieving Boyce-Codd Normal Form (BCNF) becomes significantly less common as the number of attributes increases. On the other hand, Third Normal Form (3NF) and Second Normal Form (2NF) remain relatively stable. These findings suggest that, especially for complex schemas that contains relations with more than 15 attributes(which is standard in any organization), striving for BCNF might not be worth the effort. Instead, considering how the relation is distributed, enforcing 3NF is statistically easier to achieve.
Who Should Care?
Our tool and findings are particularly relevant for database designers, researchers, and practitioners. Whether you're a database administrator seeking to optimize schema design or a researcher exploring the practical applications of database theories, FDSampleRush offers a valuable resource for empirical analysis.
In-Depth
This section contains a more detailed explanation of the paper for you nerds.
Understanding Functional Dependencies
A functional dependency (FD) defines a relationship between attributes in a relation. For example, in a table of employees, the EmployeeID uniquely determines the Name. This can be written as:
EmployeeID → Name
Meaning, for each EmployeeID, there is exactly one Name associated with it.
Let relation be a relation with attributes . An FD holds if the values of attributes in are uniquely determined by the values of attributes in , where and are sets of attributes chosen from in any combination. A relation can have any number of FDs.
Normal forms define the restrictions on FDs within a relation, guiding the process of database normalization to reduce redundancy and dependency anomalies. A relation can be determined to be in a normal form when its functional dependencies fulfill certain properties. This paper focuses on the first four normal forms: Second Normal Form (2NF), Third Normal Form (3NF), and Boyce-Codd Normal Form (BCNF).
Normal Forms Explained
- First Normal Form (1NF): All attributes in the relation are atomic (indivisible).
- Example: Each field contains only one value, not a list or set of values.
- Second Normal Form (2NF): Satisfies 1NF, and all non-key attributes are fully functionally dependent on the primary key. (i.e. for any FD , is not a proper subset of a candidate key)
- Example: In a table of orders, if OrderID determines ProductID, and ProductID determines ProductName, there should not be partial dependencies on a composite primary key.
- Third Normal Form (3NF): Satisfies 2NF, and all attributes are only dependent on the primary key.
- Example: In the employee table, separating the department head to another table where DepartmentID determines DepartmentHead.
- Boyce-Codd Normal Form (BCNF): A stricter version of 3NF where every determinant is a candidate key.
- Example: Ensuring no redundancies by restructuring tables so that every determinant (attribute determining another attribute) is a key.
Methodology
Sampling and Testing
The main functionality of FDSampleRush lies in the Choose(n, D1, D2) algorithm. Given a configurable and time limit , the Choose(n, D1, D2) algorithm samples random sets of functional dependencies for a relation with attributes and outputs the cumulative frequency distribution of each normal form. The pseudocode of the Choose(n) function is outlined below:
Algorithm 1: Choose(n, D1, D2)
plaintext1: Result ← {} 2: while time spent < t do 3: Pick a random number m ∼ D1 where 0 ≤ m ≤ 2^(2n) 4: counter ← 0 5: Σ ← {} 6: while counter < m do 7: Generate a tuple of binary words (w1, w2) where w1, w2 ∼ i.i.d. D2 and len(wi) = n 8: newFD ← (w1 → w2) 9: if newFD ∈ Σ then continue 10: Append newFD to Σ 11: counter ← counter + 1 12: end while 13: res ← TestNF(Σ, R) ∈ {BCNF, 3NF, 2NF, 1NF} 14: Append res to Result 15: end while 16: return Result
Explanation
The core idea behind Choose(n, D1, D2) is to efficiently explore the space of possible functional dependencies (FDs) by leveraging random sampling. Here, represents the distribution for the number of FDs, and represents the distribution for generating attribute sets for FDs. By sampling from these distributions, the algorithm can simulate a wide range of potential database schemas.
The upper bound of for (the number of FDs) is derived from the combinatorial explosion of possible attribute subsets for both the left-hand side (LHS) and right-hand side (RHS) of FDs in a relation with attributes. This ensures that we capture a comprehensive range of scenarios, from sparsely to densely populated FDs.
The use of binary words for representing FDs allows for efficient bitwise operations, which are critical when dealing with the exponential complexity inherent in checking candidate keys and normal forms. The representation also simplifies the process of generating random FDs, as binary vectors can directly correspond to subsets of attributes.
Technical Implementation
To accommodate the exponential nature of the candidate key-checking algorithm, we implemented several optimization strategies to efficiently compute the randomized generation process and the normal form checks of the sets of FDs.
Representation of Functional Dependency
A functional dependency for a relation with attributes is represented as a pair of binary words of length , . This translates as follows:
A binary word represents the presence of attributes in , where the -th bit corresponds to whether attribute is present. The tuple thus corresponds to the functional dependency of all attributes present in on all attributes present in , i.e., .
Example: If has 4 attributes and and , this represents the FD .
Explanation
The choice of binary representation for FDs leverages bitwise operations for efficiency. This is particularly useful for operations like subset checks and unions, which are common when testing normal forms. For instance, checking if one set of attributes is a subset of another can be done using bitwise AND operations, significantly speeding up the process compared to traditional set operations.
Additionally, the use of binary words aligns well with the inherent combinatorial nature of database schemas, allowing for a more straightforward implementation of randomized sampling algorithms. This representation is also advantageous when scaling the algorithm to handle larger schemas, as bitwise operations are inherently fast and can be parallelized easily.
Evaluation
FDSampleRush features core configurability, enabling users to customize distribution parameters, denoted as and , for the generation of FD sets. This flexibility allows for precise definitions of two critical dataset aspects: firstly, the cardinality of the set of FDs relative to the number of attributes in a relation; and secondly, the distribution of attributes in the LHS and RHS within each FD, formulated as .
Utilizing these configurable distributions, we conducted sampling and analysis on two different experiments configuring the distribution definitions to determine the influence of attribute quantity and dependency structures on the probability of a relation conforming to various normalization forms.
Experiment 1: Uniform Distribution for Cardinality of FDs In the first experiment, we analyzed the impact of FD distribution on database normalization using the following settings:
- Uniform distribution for the cardinality of the FD set: , where is the set of FDs and .
- Binomial distribution for attribute selection in FDs: The probability of choosing attributes in is (similarly for ).

This experiment aimed to clarify the effect of the number of attributes on the natural occurrence of normal forms, focusing on BCNF.
Explanation
The uniform distribution for the number of FDs ensures that each possible cardinality is equally likely, providing a broad sampling of potential schemas. The binomial distribution for attribute selection models the likelihood of each attribute being part of an FD, reflecting a realistic scenario where some attributes are more likely to participate in dependencies than others.
By using these distributions, we can systematically explore how the structure of FDs impacts the occurrence of different normal forms. The results from this experiment offer insights into the practical feasibility of achieving higher normal forms like BCNF, particularly as the number of attributes increases.
Experiment 2: Uniform Attribute Selection The second experiment used a different configuration:
- Uniform distribution for the cardinality of the FD set, consistent with the first experiment.
- Uniform distribution for attribute selection in FDs: Selection is made uniformly across the total number of attributes in .
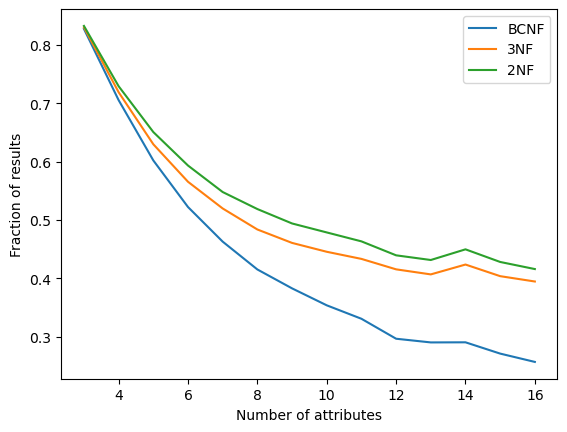
The results showed a consistent pattern of BCNF occurrence declining with more attributes, but the decline was less steep than in Experiment 1, suggesting that uniform attribute selection offers a slightly more favorable environment for achieving BCNF.
Explanation
The uniform distribution for attribute selection treats all attributes equally, simplifying the model and removing any bias toward particular attributes. This approach provides a baseline for comparison against more complex distributions, highlighting how attribute selection strategies influence the natural formation of normal forms.
The findings from this experiment reinforce the importance of considering attribute distribution when designing databases. By understanding how different distributions affect normalization, database designers can make more informed decisions about schema design and optimization.
Conclusion
The methodology implemented in FDSampleRush, with its advanced randomization techniques and efficient computational strategies, provides a robust framework for exploring the empirical distribution of normal forms. These insights challenge traditional assumptions about database normalization, suggesting a need for a more nuanced approach that balances theoretical rigor with practical feasibility. If you're interested in exploring this topic further, you can access our full project and paper here.
p.s. One last note that I think would be cool is to extend this project for dataset generation for empirical testing of FD discovery algorithms. FDSampleRush's capability to generate random sets of functional dependencies based on configurable distributions presents a nice opportunity for the empirical testing of database schemas. Future iterations of this work could focus on the generation of comprehensive datasets that simulate real-world complexities. These datasets could serve as benchmarks for evaluating the efficiency, scalability, and accuracy of current FD discovery algorithms and normalization tools, providing valuable insights into their practical applicability.